一、基本原理
CRC检验原理实际上就是在一个p位二进制数据序列之后附加一个r位二进制检验码(序列),从而构成一个总长为n=p+r位的二进制序列;附加在数据序列之后的这个检验码与数据序列的内容之间存在着某种特定的关系。如果因干扰等原因使数据序列中的某一位或某些位发生错误,这种特定关系就会被破坏。因此,通过检查这一关系,就可以实现对数据正确性的检验。 二、几个基本概念 1、帧检验序列FCS(Frame Check Sequence):为了进行差错检验而添加的冗余码。 2、多项式模2运行:实际上是按位异或(Exclusive OR)运算,即相同为0,相异为1,也就是不考虑进位、借位的二进制加减运算。如:10011011 + 11001010 = 01010001。 3、生成多项式(generator polynomial):当进行CRC检验时,发送方与接收方需要事先约定一个除数,即生成多项式,一般记作G(x)。生成多项式的最高位与最低位必须是1。常用的CRC码的生成多项式有: CRC8=X8+X5+X4+1 CRC-CCITT=X16+X12+X5+1 CRC16=X16+X15+X5+1 CRC12=X12+X11+X3+X2+1 CRC32=X32+X26+X23+X22+X16+X12+X11+X10+X8+X7+X5+X4+X2+X1+1 每一个生成多项式都可以与一个代码相对应,如CRC8对应代码:100110001。 三、CRC检验码的计算 设信息字段为K位,校验字段为R位,则码字长度为N(N=K+R)。设双方事先约定了一个R次多项式g(x),则CRC码: V(x)=A(x)g(x)=xRm(x)+r(x) 其中: m(x)为K次信息多项式, r(x)为R-1次校验多项式。 这里r(x)对应的代码即为冗余码,加在原信息字段后即形成CRC码。 r(x)的计算方法为:在K位信息字段的后面添加R个0,再除以g(x)对应的代码序列,得到的余数即为r(x)对应的代码(应为R-1位;若不足,而在高位补0)。 计算示例 设需要发送的信息为M = 1010001101,产生多项式对应的代码为P = 110101,R=5。在M后加5个0,然后对P做模2除法运算,得余数r(x)对应的代码:01110。故实际需要发送的数据是101000110101110。 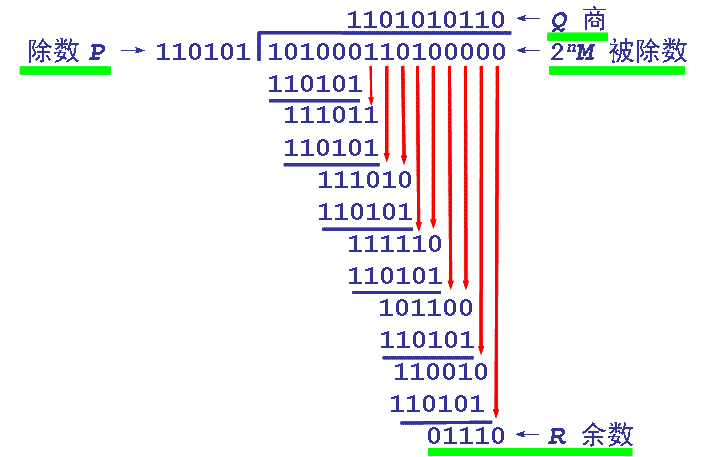
四、错误检测 当接收方收到数据后,用收到的数据对P(事先约定的)进行模2除法,若余数为0,则认为数据传输无差错;若余数不为0,则认为数据传输出现了错误,由于不知道错误发生在什么地方,因而不能进行自动纠正,一般的做法是丢弃接收的数据。 五、几点说明: 1、CRC是一种常用的检错码,并不能用于自动纠错。 2、只要经过严格的挑选,并使用位数足够多的除数 P,那么出现检测不到的差错的概率就很小很小。 3、仅用循环冗余检验 CRC 差错检测技术只能做到无差错接受(只是非常近似的认为是无差错的),并不能保证可靠传输。
线性编码理论。在发送端传送的K位二进制数据,以一定规则产生一个校验监督码(或者叫监督矩阵)r位,并负载信息后,构成一个新的二进制码序列共(K+R)位。最后发送出去。在接收端根据信息吗和CRC码禁言,是否出错。 CRC16监督式(美国标准):G(X)=X^16+X^15+X2+1 CRC16监督式(欧洲标准):G(X)=X16+X12+X5+1 一般多数采用CCITT推荐的欧标格式:10001000000100001 16位的CRC码产生的规则是先把要发送的信息元左移16位(乘以2^16),再除以监督式,最后得到的是CRC码。再把CRC码附在信息元后面,一起发送出去。 B(X).2^16/G(X)=Q(X)+R(X)/G(X) Q(X)是商,R(X)是余数。模2加减法就是不带进位借位的加减法相当异或,乘除法和普通数学乘除法一致。例如: 信息码:1011,监督元:G(X)X^8+X^5+X^4+1 CRC8校验 下面是除法运算: 1011 0000 0000 1001 1000 1 10 1000 1000 10 0110 001 11101010 所以CRC 8 监督元:11101010 发送的K+r位码:1011 11101010 接收端接收到的信息码除以监督元,如果R(X)为0,说明传输无误。 假设接收到跟发送一致。验证 1011 1110 1010 1001 1000 1 10 0110 0010 10 0110 001 0 所以接收正确无误 实际通信中发送数据是多字节,比如发送地址、控制、信息、校验。所以必须按多字节去计算CRC码。
|