2017年11月20
撰写了有关数字识别人工智能的课程设计论文,包括程序
手写数字识别 摘要 手写数字识别是机器学习领域中一个经典的问题,是一个看似对人类很简单却对程序十分复杂的问题。很多早期的验证码就是利用这个特点来区分人类和程序行为的。在手写数字识别中,比如,我们要识别出一个手写的“9”,人类可能通过识别“上半部分一个圆圈,右下方引出一条竖线”就能进行判断。但用程序表达就似乎很困难了,你需要考虑非常多的描述方式,考虑非常多的特殊情况。在本文中将从K-近邻算法(KNN)和一对多的逻辑回归算法角度进行分析。
第1章 K-近邻算法 最简单最初级的分类器是将全部的训练数据所对应的类别都记录下来,当测试对象的属性和某个训练对象的属性完全匹配时,便可以对其进行分类。但是怎么可能所有测试对象都会找到与之完全匹配的训练对象呢,其次就是存在一个测试对象同时与多个训练对象匹配,导致一个训练对象被分到了多个类的问题,基于这些问题呢,就产生了KNN。 1.1 K-近邻基本原理 KNN算法是从训练集中找到和新数据最接近的k条记录,然后根据它们的主要分类来决定新的数据的类别。具体算法步骤如下: ⑴ 算距离:给定测试对象,计算它与训练集中的每个对象的距离。什么是合适的距离衡量?距离越近意味着这两个点属于同一类的可能性越大。其中距离的衡量方法包括欧氏距离、夹角余弦等。 ⑵ 找邻居:圈定距离最近的k个训练对象,作为测试对象的近邻。 ⑶ 做分类:根据这k个近邻归属的主要类别,来对测试对象分类。分类的判定可以是少数服从多数,在上个步骤的k个训练对象中,哪个类别的点最多就分为该类。 1.2 matlab算法实现 本文中的训练样本为数字“0~9”,每个数字分别有500个样本图片,其中前400个样本作为训练集,后100作为测试集。训练集已经根据数字进行分类,并且每个图片都经过处理转化为20×20的灰度矩阵。为了计算机方便计算,将20×20的灰度矩阵化成1×400的向量形式。 %% 初始化 clear; clc; k = 7; %设置找近邻所需对象的数量 load labels load trainData [m,n] = size(trainData); %% testData a = 4; %a为第a类样本 b = 56; eval(sprintf('load C:/Users/HP/Documents/%d_%d.txt',a,b)); eval(sprintf('testData = X%d_%d;',a,b)); testData = testData';
|
|
至此我们的测试样本保存在testData中,接下来运行KNN算法。在执行KNN算法之前还需要对参数进行进行归一化处理: D = max(trainData,[],2) - min(trainData,[],2); trainData = (trainData-repmat(min(trainData,[],2),1,n))./repmat(D,1,n); testData = (testData - min(testData))./(max(testData)-min(testData)); |
|
之后调用KNN算法,并显示判断结果: relustLabel = knn(testData,trainData,labels,k); fprintf('the real number in the picture is %d\n',a); fprintf('predict number in the picture is %d\n',relustLabel); |
|
算法具体代码如下: function relustLabel = knn(inx,data,labels,k) % inx为测试集,data为训练集,labels为训练集标签,k为判断时选取的点的个数 % relustLabel为测试集的标签 [datarow,datacol] = size(data); [inxrow,inxcol] = size(inx); data = repmat(data,1,1,inxrow); inx = repmat(reshape(inx',1,inxcol,inxrow),datarow,1,1); dis = reshape(sum((data-inx).^2,2),datarow,inxrow); [kdis,ind] = sort(dis,1); %¶Ô¾àÀëÅÅÐò ind = ind(1:k,:); for i = 1:inxrow, aa = tabulate(labels(ind(:,i))); [bb,inds] = max(aa(:,2)); relustLabel(i,:) = aa(inds) ; end |
|
程序运行结果如下 1.3 小结 KNN算法简单易于理解,易于实现,无需参数估计,无需训练。但它属于懒惰算法,对测试样本分类时的计算量大,内存开销大,评分慢。可解释性差。其结果会受到K取值的影响。近邻中可能包含太多的其它类别的点。偶尔会出现错误,例如:
第2章 一对多的逻辑回归 2.1 基本原理 在分类问题中,如果要预测的变量是一个离散的值,我们将利用到逻辑回归的算法。对于一个二分类问题,我们可以利用Sigmoid函数来逼近我们的模型。函数图像如图所示: 此处 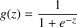 。Z可以看作是样本的分界函数,我们要对训练集做的工作就是训练出一条合理的分界函数 。Z可以看作是样本的分界函数,我们要对训练集做的工作就是训练出一条合理的分界函数 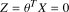 。在测试时,将测试样本的X带入得到Z的值,当Z大于0时属于“1”类,当Z小于“0”时属于“0”类。但在手写识别中,我们的训练样本一共有10类。故采用一对多的分类方法。我们将多个类中的一个类标记为正向类(y=1),然后将其他所有类都标记为负向类,这个模型记作 。在测试时,将测试样本的X带入得到Z的值,当Z大于0时属于“1”类,当Z小于“0”时属于“0”类。但在手写识别中,我们的训练样本一共有10类。故采用一对多的分类方法。我们将多个类中的一个类标记为正向类(y=1),然后将其他所有类都标记为负向类,这个模型记作 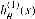 。接着,类似的我们选择另一个类标记为正向类(y=2),再将其他类都标记为负向类,将这个模型记为 。接着,类似的我们选择另一个类标记为正向类(y=2),再将其他类都标记为负向类,将这个模型记为 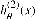 ,依此类推。最后我们得到十条不同的分界函数。 ,依此类推。最后我们得到十条不同的分界函数。 在测试过程中,我们将测试样本的X分别带入这十个分界函数  中得到Z1,Z2,Z3…Z10。若ZK>0,而其他Z都不大于0,则测试样本属于第k类。若有多个Z值都大于0则取最大的。 中得到Z1,Z2,Z3…Z10。若ZK>0,而其他Z都不大于0,则测试样本属于第k类。若有多个Z值都大于0则取最大的。 2.2 matlab算法实现 2.2.1数据处理
clear; clc;
%% 读取数据 load ex3data1.mat; for i = 1:10 % 每个数字读取前400个样本 X_train([400*i-399:400*i],:) = X([500*i-499:500*i-100],:); y_train([400*i-399:400*i],:) = y([500*i-499:500*i-100],:); end m = size(X_train,1); class_y = zeros(m,10); X_train = [ones(m,1),X_train]; %将X扩展 n = size(X_train,2); initial_theta = zeros(n,1); |
|
2.2.2调用matlab中的优化工具箱 在逻辑回归中代价函数为: 在设计代价函数的时候,为了避免出现过拟合的情况,我们往往加入了正则化,新的代价函数如下: 这样在最小化代价 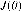 时,会让 时,会让 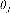 的二次项尽可能小,从而避免的过拟合的情况。 的二次项尽可能小,从而避免的过拟合的情况。 要求代价 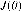 最小时的 最小时的  值,于是我们调用优化工具箱fminunc: 值,于是我们调用优化工具箱fminunc: %% 调用优化工具箱 options = optimset('GradObj', 'on', 'MaxIter', 400); lamda = 0.1; for i = 1:10; class_y(find(y_train==i),i) = 1; [theta(:,i),cost(i)] = fminunc(@(t)(costfun(t,X_train,class_y(:,i),lamda)),initial_theta,options); end |
|
其中costfun函数如下所示: function [J,grad] = costfun(theta,X,y,lamda) m = size(X,1); Z = X*theta; H = sigmoid(Z); J = -1*sum(y.*log(H)+(1-y).*log(1-H))/m+lamda/(2*m)*sum(theta(2:end).^2); thetaj = theta; thetaj(1) = 0; grad = (X'*(H-y)+lamda*thetaj)/m; end |
|
2.2.3 测试 读取上一步保存的训练参数thetazhenze。取一个测试样本,带入到 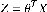 判断Z的大小。 判断Z的大小。 load thetazhenze; load ex3data1.mat; m = size(X,1); X = [ones(m,1),X]; i = 9;n = 50; %n作为偏移量在1:100中取,i作为数字类在0:9中取 H = X(500*(i+1)-100+n,:)*theta; [h,ind] =max(H); %取H中最大的标签 if ind == 10, ind = 0; end fprintf('the number is %d\n',ind) %输出结果 |
|
2.2.4 输出结果 ① 若未加入正则化,当i等于9时输出为8,发生错误: ② 若加入正则化,当i等于9时输出为9,正确: 2.3 小结 一对多的逻辑回归算法相比KNN算法增加了对训练集的训练过程,算法过程虽比KNN算法更复杂,但实际测试效果更理想。
第3章 总结 手写数字识别的方法还有许多,例如可以用神经网络进行识别。但时间有限,目前只用了这两种方法,并用代码实现,识别的准确率还有待提高。
完整的Word格式文档51黑下载地址:
 自研1703班滕翔模式识别.docx
(142.52 KB, 下载次数: 15)
自研1703班滕翔模式识别.docx
(142.52 KB, 下载次数: 15)
|