,产生这些概念的前提:正弦量被广泛采用,原因如下
1. 电力工程,发电输电用电,正弦量使设备简单,效率高,经济
2. 实验室易于产生标准的正弦量
3. 有一套成熟的正弦电路的算法
4. 正弦量可以利用傅里叶级数分解为不同频率的正弦量
对于正弦的使用以及电路分析有这样的解释:
对电路的分析其实就是对电路的建模,包括对每个元器件的建模。纯阻性元件的数学模型很简单,只有一个方程。而理想电感的方程会复杂一点,电压电流满足一个微分方程,而且还有关于磁链的方程。对于非线性的二极管等等,就有更复杂的数学模型。
数学模型建立起来之后就要求解。在求解过程中,人们发现,只有e^x和正弦函数具有一个特殊的性质,那就是不管求导多少次,都满足函数的相似性。人们就开始研究,能否把输入都用正弦信号或者指数信号的叠加代替,带入电路的数学模型之后,计算非常简便,得到输出之后,再把输出恢复成实际的信号。这就是傅立叶和拉普拉斯解法。
在用正弦信号求解的时候,指数函数和正弦函数又有一个牛逼的公式将两者联系起来,这就是欧拉公式,这样正弦函数的相位信息就可以放到指数函数中去。
所以与其相关的算法如期而至
首先,时域算法,最容易理解,首先描述正弦量的是时域的算法(其定义的时候就是用的时间,随时间按正弦规律变化的电压和电流就是正弦量)
基本的单位有:
频率,周期,角频率,瞬时值,最大值,有效值
相位(瞬时值变化进程)
初相位
相位差(前提,频率相同,反映了两个正弦量变化进程差异,而非产生波形先后,超前
滞后 同相
反相正交)
①时域——相量
(将时域分析 换为 频域分析)
细节一点,在时域的正弦表示中,根据欧拉公式,转化为了相量的形式,这其中,相量形式保持了原来正弦量的 幅值、初相位信息,即
两者联系为
通过欧拉公式 实数范围的正弦时间函数和复数范围的复指数常数一一对应

但是需要注意的是,此时,我们取到的仅仅是复指数的实数部分,而且不研究旋转因子e^jwt
,原因是,在线性的电路中,全部的稳态响应也是同频率的正弦函数,没有新的频率,w显然不是研究问题的中心,也就在相量分析中放在了一边。
两者的区别为
相量!=正弦量,只能表示两个要素(幅值与初相位),没有ω
学习了相量分析中的叠加原理和微分原理,值得注意的是,正弦量的微分为同频正弦量,对应的相量为原相量乘以
jω,但不能说,相量的导数是相量乘以jω,因为,这是对于正弦量的求导,相量不是t的函数。可以感性的了解到,对于原来正弦量的t的求导,表现在相量上出来一个与时间有关的jω也是情理之中。
使用条件
相量法只适用于激励为同频正弦量的非时变线性电路
但是为啥这叫频域分析呢?
不是已经把w给忽略了么?
可以这样理解,之所以略去,就是因为相当于强调了,我分析就是在频率不变的情况下分析的!这是一个前提!
好吧,还是知乎http://zhuanlan.zhihu.com/#/wille/19763358(00)大神膜拜

但是,前面所说的全都是一个频率,可以看做,对应频域就是一个w的正弦。
相量法之所以分离出来,在一定程度是为了区别复频域,要知道复频域里面是有s的,其中有频率的量纲,频域是以频率为变量的,而相量法是频域特殊的一种,即w直接不变了,直接叫相量法肯定更有代表性。
这应该够清楚的了
② 时域——复频域 (买噶的)
这玩意儿纠结我很久了,是该给他算账的时候了。
时域线性常微分方程经过拉氏变换到拉氏,度娘如是说。
拉式变换?啊,我的积分变换,咋么不好好学 ,坑爹的学校还不让学信号与系统。。。好吧,把人家的课程知识偷过来看看

顿时感觉是不是瞬间脑补了一下?
如果没有,解释一下:
简要的说一下啥是傅里叶和拉普拉斯,
傅里叶,一个时域的函数,通过乘上一个e^jwt
,为啥凭空乘个这东西呢?看人家后面怎么做:
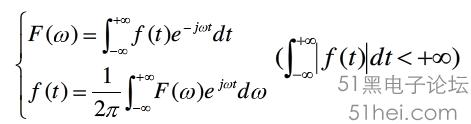
简直机智!把原来的函数在原来的t的时域上面进行积分,获得了关于w的函数,也就是频域上面的函数(请原谅我的迟到的理解,,,本应该在积分变换就应该理解的东西。。。),这样,这样就实现了对于时域与频域的变换。
而拉普拉斯,则是对于傅里叶函数成立条件太苛刻而进行的拓展,在乘以e^jwt
的基础上,直接乘以e^σ,保证原来的函数是在t的时域上面是收敛的,也就是通过积分可以获得一个不是无穷大的函数,而这个函数的变量,从原来的w,即频域,拓展到了复频域s上面,这个s不仅仅可以描述傅里叶的频率,更可以可以信号的衰减震荡稳定等关系(自控系统的稳定性分析)
两者讲完了,但是在电路分析中对应有什么呢?自控系统为毛也有这东西呢?
网上这解释比较直观:
拉普拉斯为什么可以求解微分方程?
拉普拉斯变换提供了一种变换定义域的方法,把定义在时域上的信号(函数)映射到复频域上(要理解这句话,需要了解一下函数空间的概念--我们知道,函数定义了一种“从一个集合的元素到另一个集合的元素”的关系,而两个或以上的函数组合成的集合,就是函数空间,即函数空间也是一个集合;拉普拉斯变换的“定义域”,就是函数空间,可以说,拉普拉斯变换就是一种处理函数的函数.由于拉普拉斯变换定义得相当巧妙,所以它就具有一些奇特的特质),而且,这是一种一一对应的关系(只要给定复频域的收敛域),故只要给定一个时域函数(信号),它就能通过拉普拉斯变换变换到一个复频域信号(不管这个信号是实信号还是复信号),因而,只要我们对这个复频域信号进行处理,也就相当于对时域信号进行处理(例如设f(t)←→F(s),Re>a,则若我们对F(s)进行时延处理,得到信号F(s-z),Re>a+Re[ z],那么就相当于我们给时域函数乘以一个旋转因子e^zt,即f(t)e^zt←→F(s-z),Re>a+Re[ z];只要对F(s-z)进行
电路中吧,有这些:
在这儿可以看出,有一个作用就是,求解微分方程,因为这东西把时域的东西,放在了复频域上面,变量就少了很多,首先,他本身就是积分,微分和积分本来就是克星啊(很牵强,毕竟人家高次微分方程也能解,虽然是进行一次积分),还有就是,复指数进行微分等计算的时候,形式是不变的,极为方便(可以求解高次原因?),我想这就是为什么拉普拉斯变换在微分方程上面有这么大的威力。直接靠自己的性质,活生生的把高次的微分方程变成了代数方程。
其次呢?想一下电路的使用拉普拉斯的过程可以看到,我们没直接想到使用拉普拉斯,而是先对电路进行了数学建模,得到的是微分方程,对其进行求解,这过程会用到拉普拉斯,在这个过程中,我们发现,我们可以直接跳过列写微分方程,直接在原来的电路模型上面对于电学器件进行相应的拉普拉斯变化,而且,巧合的是,正好这样列写的方程完全符合线性直流电路的求解方法。这就是在电路中使用复频域分析方法分析暂态响应。
然后,就是一直在说的频域,复频域,时域,相量分析方法,通过了前面的说明,我们可以知道,相量分析法,是频域的特殊的一种(他的频率不变);对于复频域分析方法,也就是上面一段,他是频域的拓展,不仅实现了频域的表示,可以描述信号的衰减等情况时域,再简单不过了,刚刚开始的那些。可以说,电路中频域的介绍是通过相量法进行的,让我们直接从以时间为变量的信号,直接通过巧妙的转化(欧拉公式),转化到了一种特殊的频域上进行求解,但是对于原件的等效,其实已经设计到了傅里叶变换的范畴,即电学原件在傅里叶变换中的表达形式。又因为可以看到,在后面的学习中,复频域分析与相量分析的转化中,我们是直接把s换成了jw,也就是把拉氏变换的反应信号变化的功能进行了简化,也对应于傅里叶的jw与s域的关系。好吧,,,有点啰嗦了。。上一张图吧:

最后总结一下,什么时候用相量模型,什么时候用拉普拉斯的复频域模型呢?
首先,电路的分析中,除了直流稳态分析外(基尔霍夫电压电流,神马节点电压,神马戴维南等效啥的),有正弦稳态分析(向量法),以及线性电路的暂态响应分析,对于前者我们大家都会,现在对于后者进行一下总结。
对于暂态响应的分析,给人的感觉就是,我要研究的是电流电压的变化趋势与变化过程,其中就不免有,衰减震荡,发散啊,等幅震荡等出现,上面也已经讲到,描述这些过程用复频域是再好不过的了,神奇的实部;但是对于暂态响应,还有以前的经典算法:三要素算法,卷积积分法(这个是毛线,我个弱逼,百度文库太多了)。但是疑问的是,是不是所有的暂态响应都可以使用复频域?呵呵,有些电路太简单,三要素一看就出来,就不用复频域啦吧。
我的清明节,献给了你,艾玛,好好学数学啊,弄懂了点,感觉真爽。
希望大神看到我哪有理解问题能批评指正,大神们在上,受弱逼一拜
吐一句,,,为毛学校不让我们学信号与系统。。根本不懂啥是神马域么,电气狗的悲哀