第一章 绪 论生命现象和生物的智能行为一直为人工智能研究者所关注。而自然免疫系统正是人工智能方法灵感的重要源泉之一。免疫系统在显示学习、适应性、记忆机制等应用于不同计算任务的方法方面可以给人们提供丰富的灵感和启示。从人体免疫系统发展出的计算方法已经引起许多不同领域广泛的研究兴趣。受人类自然免疫系统的启发,现在已经提出了各种人工免疫算法。人工免疫算法是模拟自然免疫系统功能的一种智能方法,它实现一种受生物免疫系统启发,通过学习外界物质的自然防御机理的学习技术,提供噪声忍耐、无师学习、自组织、记忆等进化学习机理,结合了分类器、神经网络和机器推理等系统的一些优点,因此具有提供新颖的解决问题的方法的潜力。它已经成为继神经网络、模糊逻辑推理和进化计算后人工智能的又一研究热点。
思维进化算法是模拟人类思维进化过程的一种新型进化算法,其中的趋同与异化的概念对于目前正在大量广泛研究的人工免疫算法有着重要的启示。
根据人工免疫和思维进化的特点,本文提出了人工免疫思维进化算法。该算法借鉴了思维进化中的上述特点,引入了趋同半径和异化半径的概念,这样抗体根据克隆扩增和受体编辑的原理分别进行局部竞争和全局竞争,实现了两层搜索机制。另外,算法中强调了免疫记忆的优良抗体保持作用。
第二章 免疫算法2.1一般的免疫遗传算法免疫遗传算法可以看作一种新型融合算法,也是一种改进的遗传算法,一种新型计算智能方法,是具有免疫功能的遗传算法。与免疫算法一样,把待求解的问题对应为抗原,问题的解对应为抗体,在许多方面表现出超越遗传算法和免疫算法的优点,目前应用相对较为广泛,比如神经网络设计、问题、信号分析、色谱分析、设计等等。这些算法既保留了遗传算法的搜索特性,克服遗传算法由于交叉搜索而在局部搜索特性,克服遗传算法由于交叉搜索而在局部搜索解空间上效率较差的缺点,又在很大程度上避免未成熟收敛。该算法一般形式如图一所示。
图一
免疫遗传算法与免疫算法在形式上看,就是在免疫算法中加入了遗传算子,与遗传算法相比,增加了抗原识别、记忆功能和调节功能,没有附加复杂的操作,没有降低遗传算法的鲁棒性,算法兼顾了搜索速度、全局搜索能力和局部搜索能力。免疫遗传算法一般形式只是要表明免疫机制对进化算法的作用。
免疫遗传算法的主要特点有:
1.多样性抗体
通过细胞分化,免疫系统可产生大量不同的抗体来抵御各种抗原。利用该特点可维持进化过程中个体的多样性,提高全局搜索能力,避免陷入局部最优解。
2.个体浓度的抑制和促进
免疫系统的平衡机制通过对抗体的促进和抑制作用,经自我调节产生适当数量的必要抗体。利用这一特点可提高进化算法的局部搜索能力,加快计算收敛速度,从而提高个体适应环境的能力。
3.记忆能力
免疫系统的记忆功能是当适量的抗原侵入时,免疫系统会相当准确地与之响应。以后再有不同抗原入侵时,不论数量的多少,免疫系统都会迅速而且准确地与之响应。这样能够减少搜索时间,使之快速的收敛到最优解。
4.遗传算子
在编码方案、适应度函数及遗传算子确定后,遗传算法将利用进化过程中获得的信息自行组织搜由于基于自然的选择策略为“适者生存,不适应者被淘汰”,因而适应度大的个体具有较高的生存索概率。通常,适应度大的个体具有更适应环境的基因结构,再通过基因重组交叉和基因突变变异等遗传操作,就可能产生更适应环境的后代。选择操作消除了算法设计过程中的一个最大的障碍,即需要事先描述问题的全部特点,并要说明针对问题的不同特点算法应采取的措施。因此,我们可以解决那些复杂的非结构化问题。
2.2改进的免疫遗传算法本文基于人工免疫原理,提出了一种新型的免疫遗传算法,采用二进制编码,通过引入小生境概念,将演化种群分为若干个小子群以实现种群隔离,采用了一种自适应式的选择机制,并与免疫系统的克隆选择和克隆抑制机制相结合,能够有效的促进优秀抗体的繁殖,抑制浓度过高的抗体,保证抗体的多样性,提高个体的适应度和防卜种群的退化,提高收敛速度。本算法的流程图如图二所示。
图二
2.2.1免疫记忆免疫系统中抗原消失很长时间,抗体形成细胞仍然具有免疫记忆,从而以后抗原入侵时,生物体根据自身免疫网络可以很快生成对应的抗体来中和抗原。这里我们引入该功能,计算小生境内各个抗体的适应度值,如果本次计算得到的最大适应度值大于已有的最优值,则将对应的解保存到记忆表中,否则从记忆表中选择历次得到的最优解并进行选择、交叉和变异操作,得出适应度更高的解作为免疫抗体。
生物体由于机体本身的新陈代谢,每天有的低激励值细胞死亡,而代之以从骨髓中生成全新的细胞,而且新产生的细胞只有具有较强适应性的才能融合到免疫系统中。模拟免疫行为中细胞的这种现象,算法中将小生境内的低适应度值的抗体去除,并代之以随机产生的新解。
2.2.2基于小生境技术和抗体浓度及适应度的自适应式免疫遗传选择策略1.计算抗体的适应度
即抗体i与抗原之间的亲和度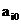 。对于求优化问题可将抗体的适应度直接取对应的目标函数值,即
。对于求优化问题可将抗体的适应度直接取对应的目标函数值,即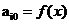 。
。
2.计算抗体i,j之间的亲和度
信息墒可作为状态分散程度的度量,因此用信息嫡来描述抗体的多样性及等位基因概率的变化进程。如图三所示个抗体。
图三
设有N个抗体,抗体长度为M,等位基因的种类为S,则N个抗体第j位基因信息嫡为:

其中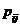 为第i个抗体的等位基因源于第j个基因的概率。如果在位置上所有抗体的等位基因都相同,那么
为第i个抗体的等位基因源于第j个基因的概率。如果在位置上所有抗体的等位基因都相同,那么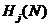 等于零。
等于零。
平均信息嫡为: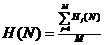
抗体i,j之间的新口度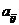 ,反应两抗体之间的相似度:
,反应两抗体之间的相似度:
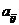 越大,表示抗体i,j越亲和。
越大,表示抗体i,j越亲和。
3.计算抗体的浓度
抗体i的浓度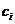 表示群体中相似抗体所占的比重。
表示群体中相似抗体所占的比重。

其中

µ为一固定值。
4.基于抗体浓度和适应度的自适应式选择策略
为保证群体的多样性,通过选择机制进行抗体的促进与抑制调节。本文中提出在每代抗体i适应值上叠加一个服从态分布的最优个体所对应的适应值,及其与该抗体的浓度相结合的方法来确定抗体i是否被选择进行以卜的步骤。抗体i的选择概率公式如下:

其中
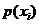 ——抗体i的选择概率
——抗体i的选择概率
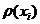 ——叠加正态分布变量的适应度值
——叠加正态分布变量的适应度值

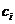 ——抗体i的浓度
——抗体i的浓度
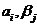 ——为自适应式的可变因子,其随着进化代数的增加而减小。
——为自适应式的可变因子,其随着进化代数的增加而减小。
基于抗体浓度和适应度的白适应式选择策略能有效的抑制浓度过高的抗体繁殖,保证了抗体的多样性,避免算法陷入局部最优值。并且,采用正态分布式的选择策略能够将优秀抗体附近的个体保留下来,减少收敛时间,提高算法的搜索速度。
第三章 基于免疫的粒子群算法寻优对于单峰值函数优化问题,算法的收敛速度是非常重要的但是对于多峰值函数优化问题,不但要求算法的快速收敛性,更重要的是要能找到全局最优解,避免陷入局部极值点。为了评价本文提出的免疫遗传算法的求解性能,与传统的简单遗传算法和一般的人工免疫算法进行了对比。由于算法的初始解群生成是随机的,只凭儿次运行结果不能说明问题,因此对所有的测试算法均独立运行次,考虑算法收敛到全局最优点的平均迭代代数,以及在这次运行中,算法收敛到局部极值点的次数经过足够大的迭代次数后仍不能收敛到最优点,就认为算法陷入了局部极值点。
3.1对已知函数的优化基于免疫的粒子群算法是在免疫算法的基础上采用粒子群优化对抗体群体进行更新,可以解决免疫算法收敛速度慢的缺点。
对于这个函数,用基于免疫的粒子群算法步骤:
1.确定学习因子c1和c2、粒子(抗体)群体个数M。
2.由logistic回归分析映射产生M个粒子(抗体)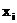 及其速度
及其速度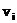 ,其中i=1,2,...,N,最后形成初始粒子(抗体)群体
,其中i=1,2,...,N,最后形成初始粒子(抗体)群体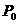 .
.
3.产生免疫记忆粒子(抗体)。计算当前粒子(抗体)群体P中粒子(抗体)的适应值并判断算法是否满足结束条件,如果满足则结束并输出结果,否则继续运行。
4.更高局部和全局最优解,并根据下面公式更新粒子位置和速度;
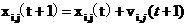


5.由logistic映射产生N个新的粒子(抗体)。
6.基于浓度的粒子(抗体)选择。用群体相似抗体百分比计算产生N+M个新粒子(抗体)的概率,依照概率大小选择N个粒子(抗体)形成粒子(抗体)群P然后转入第(3)步。
7.图五为免疫粒子群算法流程图
图四
图五为函数优化结果:

图五
图六为基于免疫粒子群优化算法收敛结果:

图六
结 论本文提出一种免疫粒子群优化算法,该算法保留了一般免疫算法的基于抗体生存期望值的选择策略,以保证抗体群体的多样性,采用了交叉和变异产生新的抗体群体。在此基础上,应用了粒子群优化对群体进行更新,本文并没有完全采用粒子群优化表达式对群体进行更新,而是根据免疫算法的特点对其进行了简化,使每个个体只跟踪全局极值,使群体进化具有更明确的方向性,从而加快算法的收敛速度。通过求解六峰驼背函数的最大值验证了算法的有效性,并将其与一般的免疫算法进行了比较。
由于本文提出的免疫粒子群算法是在一般免疫算法的基础上加进了粒子群更新而得到的,所以在运行速度上可能要慢些,但是收敛速度确实能够得到满意的性能,下一步的工作是进一步加快算法的运行速度,对算法的有效性进行更全面、更有效的验证。
附 录一在MATLAB中编写程序代码(见附件):
二建立目标函数代码:function y = immuFunc( x )
y=(cos(x(1)^2+x(2)^2)-1)/((1+(x(1)^2-x(2).^2))^2)+0.5;
End
三在MATLAB命令行窗口输入代码:[xm,fv]= POS_immu(@immuFunc,50,2,2,0.8,100,5,0.0000001,10,0.6,0.0000000000000000001,0)
参考文献[1] 曹先彬,刘克胜,王煦法.基于免疫进化规划的多层前馈网络设计.软件学报,1999,10(11):18于1184
[2] 王熙法,张显俊,曹先彬等.一种基于免疫原理的遗传算法.小型微型计算机系统. 1999,20(2): 17-20
[3] 高鹰,谢胜利.免疫粒子群优化算法.计算机工程与应用. 2004,6:4-7