固定翼无人机发展较早,在相关技术上相对比较成熟,而且在最近几十年 的几次军事战争中也充分展现了它的优秀侦查和攻击性能。与固定翼的飞行器 发展相比,旋翼式这种可垂直起降(VTOL ,Vertical Take-off and landing)的飞 行器发展要缓慢很多,最近几年随着影视拍摄行业的成功应用才慢慢进入大众 的视野,这是因为 VTOL 旋翼式的飞行器的控制比较复杂。相比于固定翼飞行器,VTOL 飞行器具有难以比拟的优越性:结构简单,更加小型化,能够适应 各种复杂的环境,具备自主起飞和着陆功能,能以如悬停、倒飞、侧飞、前飞 等各种姿态飞行,具有良好的低空低速飞行性能,对场地要求不像固定翼那么苛刻。 四旋翼直升机是一种具有四个螺旋桨的飞行器,属于多旋翼飞行器中的一种,国外又称 Four-rotor,Quadrotor, X4-flyer,4 rotors helicopter 等等。其螺 旋桨按照旋转方向的不同可以分为正桨和反桨, 四个螺旋桨按照正反桨交替的 顺序依次安装在一个具有“X”或“十”型刚性结构的末端。与传统的直升机通过调 节主桨和尾桨的桨距角来改变直升机的姿态有所不同, 目前大部分四旋翼直升机是固定桨距的,只能通过改变四个螺旋桨的转速来改变飞行器姿态,实现各 种飞行动作(目前也有变螺距的四旋翼飞行器,这种飞行器的结构相对复杂一些,但控制更灵活方便)。 小型四旋翼飞行器由于其自身小巧灵活的特点,特别适合在近地面环境中
执行监控、侦察等任务。目前已成功运用于航空影视拍摄,交通疏导,地图测 绘,抗震救灾等多个领域,有着巨大的市场前景。与此同时,四旋翼飞行器 还是美国 火星探测 项目中的 无人飞行器 重要研究方向之一[2]。另外,由于其结构简单、外观新颖、成本低廉、 飞行控制方式 独特(通过调节 4 个螺旋桨的转速, 实现飞行控制)以及性能卓越等诸多优点,使其逐渐成为国际上新的研究方向。 随着近年来空中机器人相关领域技术的进步,尤其是关键传感器的小型化 和通信技术的发展,四旋翼飞行器的发展十分迅速,大家对空中机器人在工业 和生活中的应用兴趣逐步提高,小型四旋翼无人机正在广泛应用于民用基础设 施检查(如公路、桥梁和大坝),环境监测 (如森林、河流、湖泊等),飞行表演,
以及航空拍摄中。由于四旋翼飞行器是一个典型的多输入多输出非线性系统, 在飞行器飞行过程中各通道间有很严重的耦合特性,使得飞行控制器设计变得 十分复 杂, 像传 统的 控制器 如增 益调 参 [3] 的小扰 动 线 性设 计方 法 已经 很难 适 用,寻找更好的控制方法具有很重要的现实意义。
1.2 研究现状
1.2.1 四旋翼飞行器的研究现状
四旋翼飞行器自问世以来已经有将近百年的历史,由于其自身的工作方式, 导致旋翼式飞行器的能源利用率不高,续航时间和飞行半径较短,一直没有引 起足够的关注。随着近年来微机电系统(MEMS)传感器测量精度的提高,低 功耗高性能处理器技术的进步,锂电池存储密度的提升,以及新型的高强度轻 便材料的应用,都为四旋翼无人飞行器的 发展提供了强有力的硬件支持。与此 同时,四旋翼无人飞行器在军事和商业领域的应用也不断被挖掘,未来也将会有更多的应用场景被发现,其商业价值也逐渐显现 ,市场需求量很大,前景广 阔。
目前的国内外研究的四旋翼飞行器大体上都属于微小型 无人飞行器 , 其研究主要集中在以下三个方面:基于惯性导行的 飞行控制[4],基于计算机视觉 的 飞行 控制[5]和自主飞行器 系统方案 。其 典型 代表分别是:瑞士洛桑联邦科技学院(EPFL)的 OS4[5],佐治亚理工大学的 GTMARS[6]和宾夕法尼亚大学的HMX4[7]。OS4 已经完成了两代样机,是由 EPFL 自动化实验室开发的一种小型四旋 翼飞行器,其第二代样机如图 1-4 所示。针对飞行器的飞行特点,对其控制算 法进行了深入的研究 ,目前 已经实现了基于多种控制算法 ( 如 PID , LQ , Backstepping,Sliding-mode)[8]的飞行实验,可以实现自主悬停控制。HMX4 在机械机构上与 Draganflyer III 相似,利用双摄像机的计算机视觉来获取飞行器的姿态和位置,使用 Backstepping 和反馈线性化的控制算法实现 了自主悬停控制,并且在多机编队等协同合作方面取得了突破性进展,其样机 图如图 1-5 所示。

佐治亚理工大学的开发的 GTMARS 无人机系统是为实现火星探测任务而 设计的,该飞行器登陆火星后能够自动展开被封装的四面体机构,实现自主起飞和降落,样机图如图 1-6 所示。其着落器上安装了太阳能电池,在执行探测 任务时可以返回着陆器补充能量。
近年来,国内外很多研究人员开始研究多旋翼无人直升机,并且发表了大 量相关论文,也提出了很多无人直升机控制算法。并且国外很多高校已经成功 实现了其算法在硬件实验平台上的飞行控制。
目前,大部分无人直升机控制算法可大致分为以下两类:
(1)基于经验的控制算法:PID 控制[9],神经网络控制[10],模糊控制等;
(2)基于模型的控制算法: 滑模控制[6],鲁棒控制[6],Backstepping[11],
LQR[12]控制等。 由于多旋翼飞行器的外环位置直接受内环姿态的控制,所以飞行器的内环姿态控制就显的尤为重要,所以目前国内外很多研究都着重进行了非线性的姿 态控制器设计,虽然仿真效果比较好,但由于其对模型有很强的依赖性,当模 型不够精确时,其实际控制效果有时还不如基于经验的 PID 控制。因此,应寻 找既可以精确控制飞行器,又具有良好的环境自适应能力和不依赖于系统精确 数学模型的控制算法。
1.2.2 迭代学习的研究现状
学习能力是人作为智 慧生物的一项重要特 征,让控制器具有 某种“学习能 力”,一直是诸多自动控制研究者一个梦寐以求目标。自从 Fu[13]于 1971 年在控 制中提出学习的思想后,各国学者对学习 控制 的研究一直很活跃,像神经网络, 人工智能,迭代学习,强化学习等智能控制越来越受大家关注。迭代学习控制 作为智能控制领域的一个分支,在控制的学习过程中不需在线辨识系统模型参 数,而是根据最终的所达到的控制效果,既依靠“控制品质”来修正 控制器参数 。 日本研究者 Uchiyama[14]针对高速运行的机械手的控制问题于 1978 年开创性的 提出了迭代学习的控制思想:对同一个轨迹进行跟踪控制,并每次根据上次的 控制结果不断调节控制输入,最终达到比较好的的跟踪控制效果。基于这一基 本思想,Arimoto 等人在 1984 年正式提出迭代学习控制的概念[15],从此开创了 一个新的研究方向,吸引越来越多的研究者加入。
迭代学习控制方法主要是利用控制系统的先验数据,以及系统期望的输出 信号来寻找理想的控制输入信号,减小系统的跟踪误差,类似于人的“经验学习” 过程。迭代学习控制与鲁棒控制类似,迭代学习控制可以处理实际系统 模型的 不确定性,相比较而言,它要求系统较少的先验知识,不依赖于非常精确的系 统模型,能够处理未知参数以及模型的不确定性等复杂 的控制问题,具有很强的鲁棒性。因此,对那些轨迹跟踪控制中有着高度非线性,难建模等特点系统 的有着非常重要的研究意义。
目前迭代学习控制思想已广泛应用在各种工业生产中,对机械臂和机器人 系统的控制是其最主要的应用领域[16],同时在各类实时控制的系统中,迭代学 习控制也得到了广泛的应用,例如永磁电机控制 [17],磁盘驱动器控制[18],光学 扫描系统[19]等等。随着迭代学习控制理论研究的不断深入和发展,以及其在实际系统的广泛应用,迭代学习控制越来越多的与其他控制方法相结合,由此产 生了各种新的算法,如自适应学习律[20],模型参考学习律[21],基于优化理论等
的新型学习律[22],不再局限与传统的 P 型、D 型学习律。
1.3 主要研究内容
由前文介绍可以看出,未来多旋翼无人机由于其自身的优点会拥有更广阔 的前景和应用空间,会吸引越来越多的国内外的学者和研究机构加入。 由于四 旋翼无人机的强耦合、非线性、欠驱动的系统特性,再加上飞机的震动和飞行 的大机动性,导致飞控系统的姿态测量和控制设计相对较为复杂。本文将以小 型四旋翼直升机作为课题研究平台,针对轨迹跟踪控制算法和多传感器数据融 合方法进行研究,对基于迭代学习的轨迹跟踪控制算法进行仿真验证,同时对 飞行器硬件控制系统进行设计。
本文的研究内容如下:
(1)首先介绍 四旋翼无人机 的研究背景,发展现状,以及迭代学习控制的 发展,针对多旋翼飞行控制系统的设计,分析其中两个关键问题,之后提出了
本文的主要研究内容。
(2)接着介绍四旋翼无人直升机的基本工作原理及相关知识,定义建模和 控制所需的两个坐标系和对应的坐标旋转矩阵,介绍欧拉角与四元数的两种不
同的姿态表示方法,并建立四旋翼飞行器的动力学模型 。
(3)之后进行轨迹跟踪控制算法仿真研究。介绍迭代学习控制算法的基本 思想和流程,在确定的四旋翼动力学模型的基础上进行 模型简化处理,确定飞 机的飞行轨迹并生成初始输入。用卡尔曼滤波对由系统模型误差产生的扰动进 行估计,运用优化理论的迭代学习的更新算法更新系统输入,补偿系统由于模 型误差带来的重复性扰动,并用 Matlab 软件仿真进行学习算法的评估,并给出 仿真实验结果。
(4)再接着进行硬件平台设计及多传感器的数据融合。在搭建的四旋翼飞 行控制器的硬件实验平台的基础上,分析所以惯性传感器的特性,进行传感器标定,补偿由于传感器制作工艺带来的测量误差,并运用基于四元数的间接卡 尔曼滤波器抑制由于机体震动以及飞机大幅运 动对姿态估算的扰动,并对滤波 器进行故障检测与隔离,给出最终的实验结果。
(5)最后,本文将总结我的课题所做的研究工作,并对 未来进一步需要完 善和发展的工作进行展望。
第 2 章 四旋翼工作原理及相关知识
2.1 引言
四旋翼无人直升机的动力学模型是后期飞行控制算法研究的基础和前提,模 型的正确性对控制系统的设计至关重要。本章首先简单介绍四旋翼飞行器的基本 工作原理,同时定义机体坐标系与惯性坐标系的的坐标变换矩阵,并根据刚体力 学知识和牛顿定理建立系统的数学模型。
2.2 四旋翼飞行器工作原理
四旋翼无人直升机是四个螺旋桨固定在一个“X”或“十”型刚性结构的末端的 系统,如图 2-1 所示,飞行系统的螺旋桨对称分布于机体前、后、左、右四个端点, 这四个旋翼共处于同一平面上。飞行的动力来源于四个电机带动螺旋桨高速转动, 通过调节四个螺旋桨的转速可控制四旋翼飞行器的姿态和轨迹。相对的一对旋翼 2 和 4 绕逆时针方向旋转,相反另外一对旋翼 1 和 3 则绕顺时针方向旋转。改变 1 和 3 螺旋桨的转速可以产生俯仰以及相应的前向运动,同理,改变 2 和 4 螺旋桨 的转速可以产生相应的横滚和侧向运动,由此产生飞机升力及姿态的控制力。
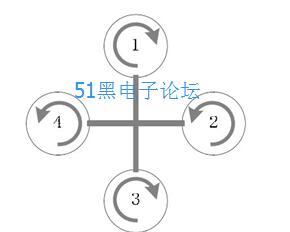
图 2-1 四旋翼直升机桨翼旋转示意图
由于四旋翼直升机在空间中的具有六个运动自由度,但是仅有四个驱动输入, 改变任何一个螺旋桨的转速都会引起两个姿态角的变化,因此四旋翼直升机是一 个欠驱动的系统[23]。根据四旋翼无人直升机的结构特点和四旋翼的姿态变化与各 个旋翼的旋转速度的关系,其基本运动可以划分为以下四个基本运动模式:
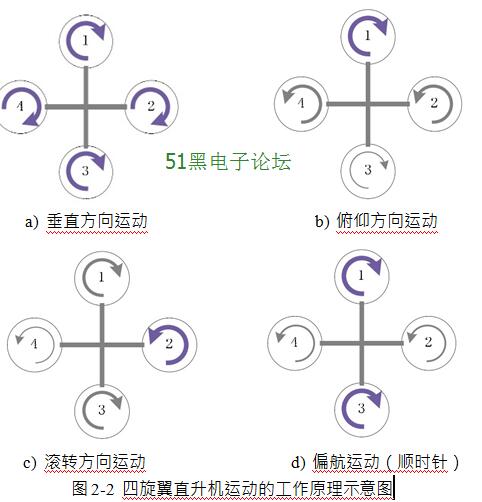
(1)垂直方向运动:主要有垂直升、降和悬停三个飞行状态,当四旋翼机身 处于平衡状态时,同时等量的增大(或减小)四个旋翼旋转速度的大小来实现直升机上升(或下降)运动,如图 2-2 a)所示。
(2)俯仰方向运动:保持旋翼 2 和 4 的转速恒定,增大(或减小)旋翼 1 的 同时减小(或增大)旋翼 3 的转速,而四个螺旋桨总的升力保持不变,会产生沿 y 轴方向的扭矩,这样就可以实现四旋翼的俯仰运动,由于耦合的作用,同时可以 实现飞机的前后方向的运动, 如图 2-2 b)所示。
(3)滚转方向运动:保持旋翼 1 和 3 的转速恒定,增大(或减小)旋翼 2 的 同时减小(或增大)旋翼 4 的转速,会产生沿 x 轴方向的扭矩,这样就可以实现四旋翼的横滚运动,同理,由于耦合的作用,可以实现飞机的左右方向的运动, 如 图 2-2 c)所示。
(4)偏航方向运动:增大(或减小)1、3 旋翼,同时减小(或增大)2、4 旋翼的转速,利用正反桨产生的相反方向的扭矩,可以改变直升机机体绕 z 轴总 体方向的扭矩,从而实现直升机偏航运动,如图 2-2 d)所示。
2.3 刚体空间姿态表示
2.3.1 常用坐标系的定义
宇宙中一切运动的物体都是相对而言的,单个物体是没有运动可言的。一个 物体在空间中的位置和姿态是相对另一个物体而确定的,这就有了参考坐标系的概念。为建立四旋翼直升机运动学模型以及进行姿态控制,首先介绍后文所需要 的两种常用坐标系的定义:
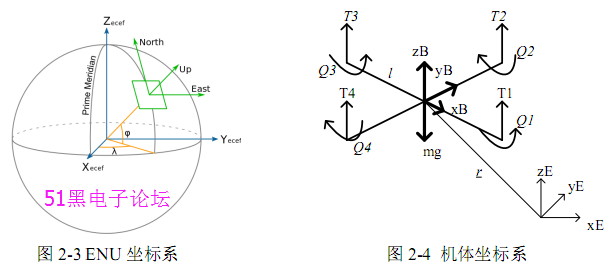
(1)东北天坐标系 E(NEU),在地面指定一个点为参考原点,取水平面为 XOY 平面,以东方向为 X 轴正方向,顺时针 90 度方向的北向为 Y 轴正方向,以垂直 水平面向上的方向作为 Z 轴正方向,如图 2-3 所示。
(2)机体坐标系 B(OXYZ),以四旋翼直升机的质心为原点,旋翼 1 和 3 的连
线为 x 轴,旋翼 1 指向为 x 轴正方向,旋翼 2 指向为 y 轴正方向,以过原点且垂 直于 xoy 平面的向上的直线作为 z 轴正方向,如图 2-4 所示。机体坐标系与飞行器固连,随飞行器的运动而转动。
2.3.2 刚体姿态角表示
刚体在空间中相对参考坐标系的形态即为刚体的姿态,它描述了两个坐标系坐标轴之间的相对方向。刚体从一个姿态到另一个姿态之间的转换可以用两个坐 标系的相对旋转变换矩阵表示。姿态表示有多种表示方法,包括四元数、欧拉角、 欧拉轴/角和方向余弦矩阵等,各种表示方法有自己优缺点,目前常用的表示方法为前两种。欧拉角表示方法最大的优点是简单直观,只需用 , , 三个参数分别表
示横滚角,俯仰角和偏航角,符合人的直观感受,缺点是不能表示刚体的全部姿 态,有奇异性,存在万向锁问题,并且在计算过程中有大量的三角函数运算,计 算量较大;四元数表示法不存在万向锁问题,而且计算量小,现广泛应用于航空 航天领域以及三维动画制作领域,缺点是不够直观,每个参数没有实际的物理意 义。下面将分别介绍这两种姿态表示方法:
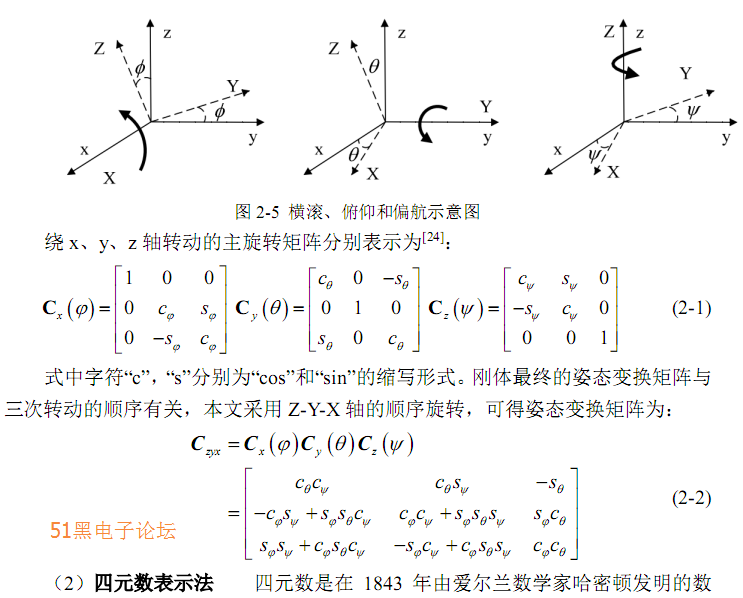
(1)欧拉角表示法 欧拉角是用来描述刚体在三维欧几里得空间的取向。 对于任何参考系,一个刚体的取向,是依照顺序,从这参考系,做三个欧拉角的 旋转而设定的。所以,刚体的取向可以用三个基本旋转矩阵来决定,图 2-5 描述了 绕三个轴的基元旋转。




(由于格式限制,51hei省略了部分内容,论文完整内容请下载本帖附件查看)
由于迭代学习过程不依赖于精确的数学模型,我 们可以忽略系统的高阶小 量,对公式(2-15)所表示的动力系统进行简化处理,原系统的状态空间方程可表示为公式(3-21)所示的系统。对于公式(3-21)所示的系统,在参考轨 迹领域内进行线性化处理:
对上述系统进行离散化后就可得到迭代学习所需要的 邻域方程。考虑到系统模型的不准确性,在轨迹跟踪过程中我们不能完全跟踪中间的姿态角状态以 及速度状态,同时由于我们的最终目标是对飞行器的位置进行跟踪,所以目标函数(3-18)中的状态权重矩阵 S 中只有位置状态因子有效,其他因子取零 , 同时不考虑输入的惩罚函数。取位置误差:
接下来利用 Matlab 软件建立的四旋翼无人直升机的仿真平台,对迭代学习 控制算法进行仿真验证,图 3-3 给出了设定参考轨迹为正弦线和圆时的迭代学 习的控制的效果图,图 3-4 为每次迭代学习的控制的位置跟踪误差。
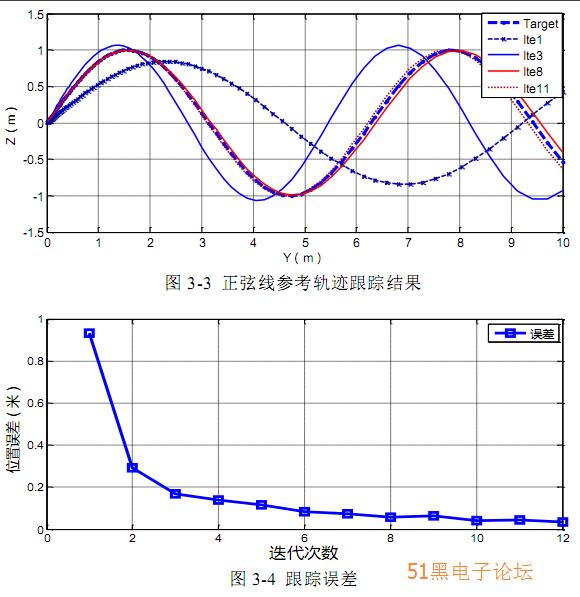
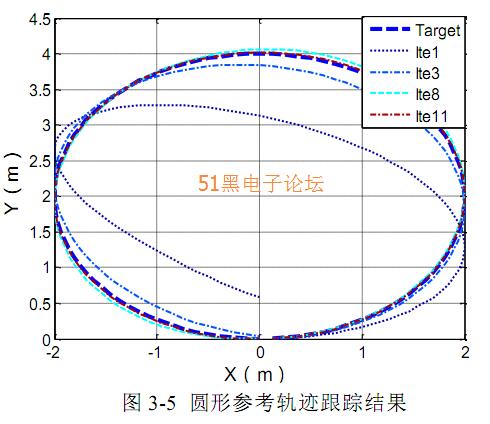
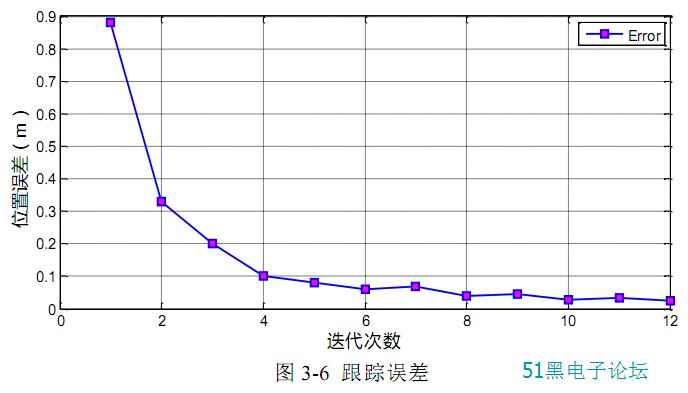
从上图中的正弦线轨迹跟踪效果图可以看出,通过多次的 迭代学习后,系 统能够很快估计出系统的建模误差,在下次迭代学习时对系统输入进行补偿, 最终能够较准确的跟踪上参考轨迹。同时,对圆形轨迹进行仿真验证。 图 3-5 中给出了设定为圆形参考轨迹时 飞行器在迭代学习控制算法下的跟踪效果,经过多次迭代学习,系统能很好的 跟踪参考轨迹。从图 3-6 可以看出,经过多次迭代跟踪误差不断减小。
3.3 本章小结
本章主要研究 四旋翼 无人直升机的基于迭代学习的 轨迹跟踪控制 算法,根 据 四旋翼 直升机的关键动力学模型,从迭代学习的控制算法的理论出发,结合 卡尔曼滤波的最优估计特性,估计出系统的重复性扰动和未建模误差。选取基于时域内二次性能函数离散方程的最优迭代学习算法,对估计出的模型误差进 行扰动补偿,对算法的轨迹跟踪性能进行了仿真验证, 通过仿真给出了四旋翼 无人机的各种轨迹下的跟踪结果,证明了算法的有效性。
第 4 章 硬件搭建及多传感器数据融合
4.1 引言
在前期完成四旋翼无人机的轨迹跟踪控制算法后,接下来课题的重点工作就 是建立飞行控制器的硬件实验平台,完成实际四旋翼飞控的硬件平台的设计。在 本章中,首先给出了飞控系统主要部分的硬件电路设计和程序设计的流程图。而 在实际的工作环境中,MEMS 传感器由于其自身的特点,虽然价格低廉,但由于 自身的工艺,传感器自身有着很大的测量误差,再加上飞行器飞行过程中的震动, 传感器的测量值需要很好的处理才能得到我们所期望的姿态角度,因此需要对传 感器的特性进行分析,并设计滤波器才能得到较精确的飞行姿态,只有姿态角度 测量准确了,才能达到较好的控制效果。本章针对硬件平台所面临的问题,首先 对电子罗盘与加速度计进行标定,分析传感器特性,对关键的传感器(陀螺仪和 加速度计)进行采样分析,进行基础的滤波处理,然后用卡尔曼滤波进行姿态更 新,最终得到较为准确的姿态数据。
4.2 飞行控制器硬件平台搭建
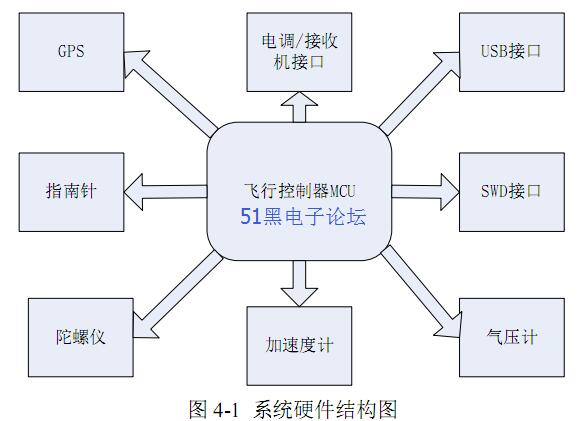
图 4-1 为系统的硬件架构图,主要由主控芯片,传感器接口,USB 接口,GPS模块接口,接收机接口以及电调接口等部分,图 4-2 为整个飞行控制系统的原理图。
本课题所使用的飞行控制器 MCU 是意法半导体公司生产的基于 Contex-M4
内核的 32 位处理器 STM32F407 芯片,该芯片拥有 168MHz 的主频,处理速度可 达 210DMIPS,同时控制器内部集成了单精度的浮点运算单元和 DSP 指令,运算速度大大提升,可以运行一些更复杂的算法。 这款芯片拥有丰富的外设,包含多种通讯接口,如 USART 串行同步异步接口,
IIC,SPI,CAN 总线等,可以与飞行控制系统所多要的多种类型的传感器直接相 连,不需要额外的通信协议转换芯片,同时这些通信接口还可以作为数据回传的 接口,可以和地面采集系统直接通信,大大简化了系统的硬件设计和系统复杂度。 并且片上具有多个内部定时器,其中的高级定时器[32]具有 PWM 波形发生器的功能,可以精确输出PWM波形而不占用CPU任何处理时间,因此能够通过定时器生成的 PWM 波 精确控制四旋翼直升机四个电机的转速 。另外,此芯片不仅支持标 准的 JTAG 下载,还支持四线制的 SWD 接口供程序下载及调试,这样可以占用更 少的芯片引脚,而且 SWD 接口在高速下载的情况下更加稳定。芯片的 I/O 口多支 持引脚复用功能,大大提高了硬件设计的灵活性。该芯片还支持高速 USB-OTG 功 能,传输速率最高可达 480Mbps,使用其 Host 功能可将主控作为 USB 主机,进行 数据的采集。整个系统的电路原理图如图 4-2 所示,系统的硬件测试平台如图 4-3 所示。
4.3 传感器标定
图 4-3 硬件测试平台
在飞机的姿态估算过程中,加速度计和磁力计的测量值将作为测量数据直接参与计算,其测量值的误差直接影响姿态跟新的准确性。而由于 MEMS 传感器的 制作工艺等原因,传感器原始输出的测量值与真实值存在较大偏差,其误差模型 如图 4-4 所示。
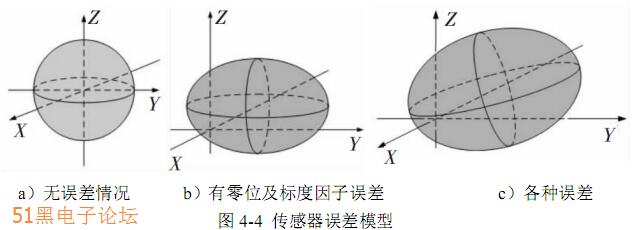
下面就以三轴磁强计为例分析误差产生原因。三轴磁强计的测量误差主要来自以下四个个方面[33]:
(1)零位偏差和灵敏度误差;
(2)非正交测量误差(三轴磁力计的测量轴不能完全正交);
(3)非对准误差(三轴磁强计的三个坐标轴与飞行器本体的坐标系不能完全重合);
(4)硬磁干扰,软磁干扰(软磁干扰误差可等效为非正交误差,灵敏度误差 和非对准误差的综合表现)。
在理想情况下,磁力传感器在空间中旋转时三个轴的理论测量值 X,Y,Z 是 一个标准的球面。由于上述误差的存在,传感器的输出将变为一个倾斜的椭球, 为了消除传感器由于自身工艺造成的测量误差,本文使用基于约束的最小二乘椭球拟合方法将磁力传感器三个轴的测量值映射为一个椭球面,然后将传感器输出 矫正为一个标准的球面。
二次曲面的一般方程为:


为了对原带等式约束的优化问 题进行求解,我们运用拉格朗日乘子方法将原优化问题化为带非线性约束的求解 特征值和特征向量的问题:
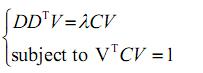
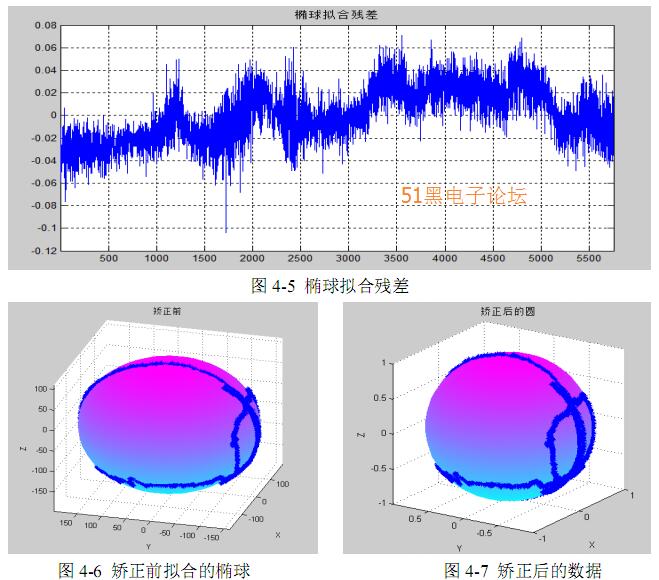
经过椭球矫正后的实验结果如图 4-7 所示。从图 4-5 中可以看到,椭球拟合的 残差很小,与真实值很接近,经过矫正后的输出是一个标准的球面,算法很好的 补偿了由于传感器的零位偏差,灵敏度误差以及各个轴之间的非正交误差带来的 影响。同理,也可用此方法对加速计进行标定。
4.4 艾伦方差分析
惯性传感器的测量误差除了由于传感器自身的制造工艺造成的标度因子,非 正交等由敏感物理模型中的参数变化引起的确定性误差外,还有敏感环境干扰这 种不确定因素引起的随机误差,主要有零偏不稳定性、角度(速度)随机游走、 速率随机游走等。随机误差由于在各个时刻的具有随机性,因此无法像确定性误 差那样通过固定的方程进行直接补偿,需要实验通过统计的方法来分析误差特性。 最常用的随机误差建模方法有艾伦方差分析法[34]、时间序列分析法和功率谱密度 分析法(PSD)。
艾伦方差分析方法是一种时域分析方法,它同 PSD 之间存在积分转换关系。 艾伦方差最早是由 David 于 1966 年提出的,最初用于分析振荡器的相位和频率不稳定性。由于陀螺仪等惯性传感器本身具有振荡器特性,所以后来艾伦方差被广
泛应用于惯性传感器的随机误差辨识[35]。相对于其他分析方法,其最大的优点是 计算比较简单,较容易对惯性传感器中的各误差源进行辨识和分离。下面以角速度为例说明艾伦方差的定义与计算。
以采样周期 对陀螺仪输出角速度进行采样,共采样 个点,把所获得的数 据分成 组,每组包含 个采样点:
使用飞行器上所用的惯性传感器,将数据输出速率设定为 100 Hz,将惯性传 感器静止放置,采取 4 个小时的陀螺仪和加速度计的原始数据,然后对采集的数 据进行艾伦方差分析,分析的结果分别如上图 4-9 和图 4-10 所示。
陀螺仪和加速度计的随机误差主要包括零偏不稳定性、角度随机游走和速率 随机游走,假设随机误差中各种误差源相互独立,艾伦方差可以表示为如下简化 形式:通过对原艾伦方差进行拟合,就可得到 Allan 方差系数,最终的分析结果如表
4-1 和表 4-2 所示,从表 4-1 中可以看出陀螺仪的 x 轴相对其他两个轴性的零偏不 稳定性要差很多,其对应后面的卡尔曼滤波器中对应的陀螺仪零偏不稳定性的过程噪声也要大很多。同样,从表 4-2 中可以看出,加速度计的 z 轴的零偏不稳定性 相对其他两个轴要差很多。
4.3 滤波器设计
4.3.1 低通滤波器设计
前面总结了惯性传感器的测量误差,其中包括确定性误差和随机误差,这两 者主要是由于传感器自身的特性所引起的,在实际的飞机飞行过程中,除了要了 解传感器的自身特性外,还需要对惯性传感器的工作状况进行分析。在飞行器飞行过程中,由于电机带动螺旋桨高速转动,若电机与螺旋桨的动平衡达不到完美效果,在飞行过程中会产生很严重的高频震动,采集飞机近似悬 停的加速度数据如图 4-11 所示。对采集的原始信号进行傅里叶变换[38],其频谱特性如图 4-12 所示,从图中可以看出采集的信号中包含了很多高频噪声,飞行器的运动频率通常小于 10 Hz[39]。
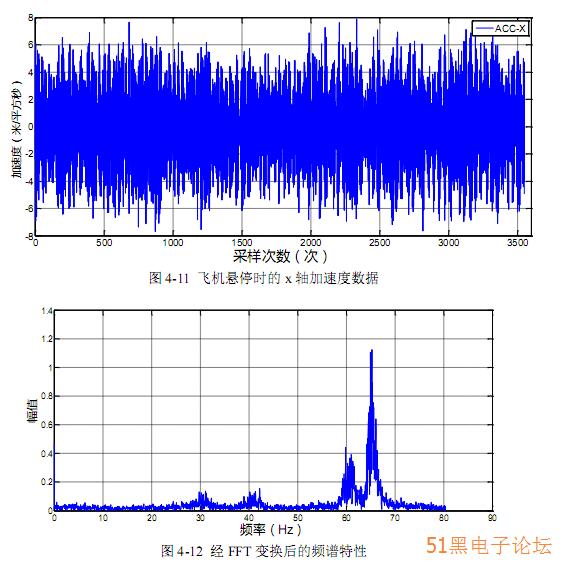
由图 4-12 可以看出,在飞行过程中,飞行器在 60~70 Hz 之间有很强的高频震 动,通过设计一个 FIR 低通滤波器就可以对其高频噪声进行初步的滤波处理。用 Matlab 自带的 FDATool 工具箱设计一个截止频率为 25 Hz 的 FIR 低通滤波器,滤 波后的频谱特性与数据如图 4-13 所示。经过所设计的 FIR 低通滤波器后,传感器 所采集数据的高频噪声被有效的滤除,在一定程度上可以消除飞行器的震动对传 感器测量的影响,可以提高后期的姿态解算精度和控制效果。
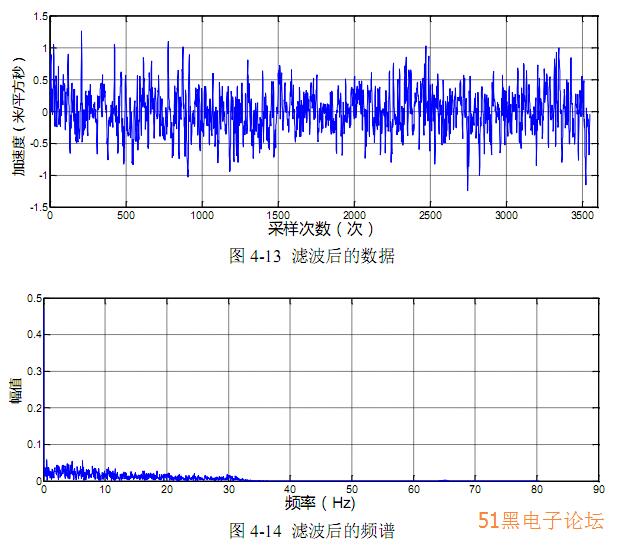
4.3.2 卡尔曼滤波器设计
飞行器准确的姿态求解是飞行器整个软件部分中的重要一环,在前面部分, 我们已经完成了传感器的标定,低通滤波器的设计,这些过程可以尽可能的减少 单个传感器自身测量造成的误差,但是为了得到最终飞行器姿态,还需要更好的 多传感器数据融合算法。
对于目前常用的 MEMS 的惯性传感器,陀螺仪的动态性能比较好,但由于温 飘和零偏,长时陀螺仪积分会造成很大的累计误差,而加速度计和磁力计计算出 的飞行器姿态无这种累计误差,不存在长时间漂移问题,但容易受环境和飞行器 飞行状况影响。我们采用高效的递归滤波器—卡尔曼滤波,结合各传感器的特点,
估计出飞行器的姿态。在滤波器的设计过程中,根据系统状态的选取不同,滤波 方法有直接法和间接法两种[40]。两种方法的卡尔曼滤波器的特点有所不同:
(1)直接法是直接描述系统的动态过程,系统方程多为非线性,因此只能采 用非线性卡尔曼滤波器;间接法的系统方程一般是按照近似方法推导出来的误差 方程,一般可以转化为线性方程,因此可以直接采用常规的线性卡尔曼滤波器。
(2)经过系统化简,相对于直接法,间接法可以减少系统维数,减小计算量。
同时,间接法所描述的状态多为误差量,数量级较为接近,可以减小计算误差。 因此,本文采用间接的卡尔曼滤波器。卡尔曼滤波是一种高效的递归估计,它无需记录观测或者估计的历史信息,本身是一种最优化自回归数据的处理方法, 整个迭代过程比较简洁,非常适合作为 AHRS 的滤波算法。将卡尔曼滤波用于多 传感器的数据融合时,首先需要建立一个符合卡尔曼滤波器算法的系统状态方程 和观测方程。
陀螺仪,加速度计,磁力计的测量模型为:
适用于卡尔曼滤波算法的线性模型就已经建立,整个间接卡尔曼滤波算法的
结构图如图4-15 所示:
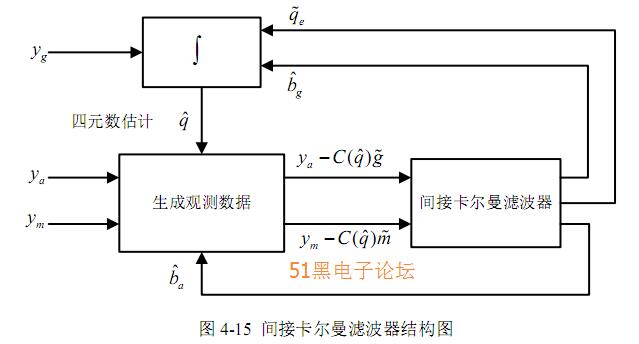
4.3.3 多传感器数据融合结果
在前面小节中,首先介绍了传感器数据的预处理部分,包括传感器矫正和 FIR 滤波器,然后介绍了卡尔曼滤波器的结构设计及实现过程,本节主要对间接卡尔 曼滤波算法的姿态融合结果进行数据分析,评估滤波器效果,并对实际飞行器飞 行过程中出现的滤波器故障进行检测与隔离,提高卡尔曼滤波器的准确性和稳定 性。首先做地面震动实验,对飞控解锁,推油门至飞行器接近起飞状态,采集传 感器数据并进行数据融合后的结果如图 4-15 所示。在实际横滚角一直接近于零度 的情况下,由于飞机的震动,直接用加速度计得到的横滚角有很大的波动,最大 可达 9 度,由于陀螺仪存在零偏,其直接计算的角度也很快会发散,用本文所提 出的卡尔曼滤波算法计算得到姿态角度一直非常平稳,误差很小,没有发散现象。
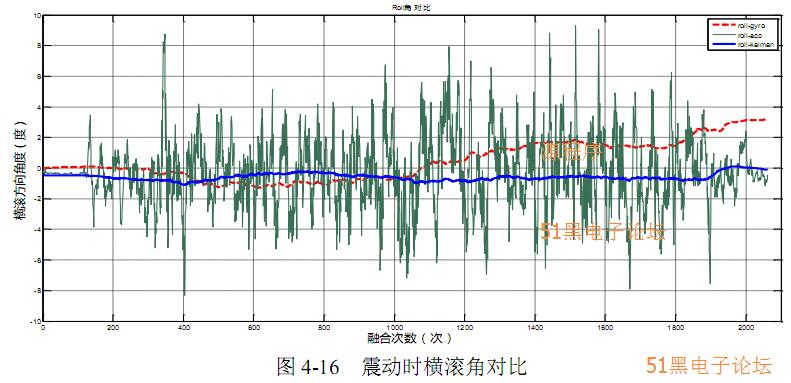
在姿态更新的过程中,同时对陀螺仪的零偏进行估计,零偏估计的结果如图4-17 所示,在经过一段时间的滤波器稳定后,滤波器很快估计出陀螺仪的零偏, 并稳定在某个常值附近。
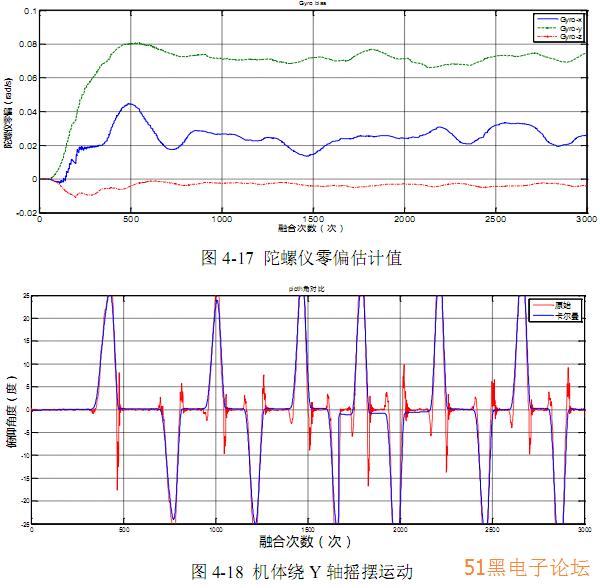
接下来我们测试飞行器做大角度运动时的解算的姿态角度是否准确,利用三楼运动控制实验室的 UR 机器人,我们将飞行控制器固定在机械臂的末端(如图4-3),让机械臂绕 Y 轴做往复摇摆运动,原始数据与卡尔曼滤波后得到的俯仰角 如图 4-18 所示,在模拟飞行器做突加(减)速运动时,由于加速度计包含了很大 的运动加速度,原始姿态角有很大的超调,并伴随有震荡现象,经过卡尔曼滤波 处理,可以消除由于突加(减)速运动的影响,使得所计算的姿态角度快速响应 而无超调。
在飞行器实际飞行过程中,飞行控制系统的稳定性是至关重要的,因此,滤 波器的容错设计也是需要考虑的。容错设计的目的是在每一个元部件稳定性一定的情况下,提高系统整体的可靠性。容错设计的主要方法是实时监测系统的运行 状态,对故障部件进行检测并进行有效隔离,防止整个滤波器发散。
故障检测与隔离(FDI)是一项专门的技术,近年来已有很大发展,在系统硬 件固定的情况下,从卡尔曼滤波器的更新过程可以进行故障检测与隔离,在这里 可以用卡方检验来确定系统量测信息的有效性[44],进行观测新息的故障检测与隔 离,与卡尔曼滤波相结合可以很好的抑制传感器测量的野值对滤波器的影响,下面具体说明基于残差的卡方检验法[45]对滤波器的故障进行检测和隔离 。
卡尔曼滤波器 的残差[46]可表示为:
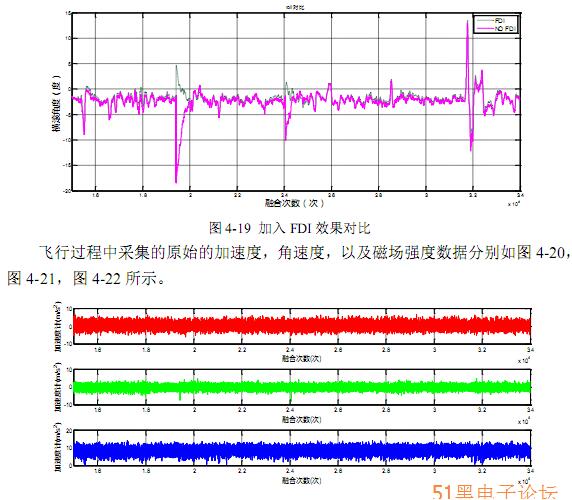
对加速度计和磁力计的量测信息分别设计一个局部的滤波器,在每一个传感 器的量测更新过程中都加入上述的故障检测与隔离算法,即可实时确定出失效的 量测信息,这样就可以剔除传感器采集的野值对滤波估计的影响。如图 4-19 所示,在某次飞行测试中,由于传感器测量异常,导致飞行姿态的横滚角有两次出现了 异常状况,加入故障检测与隔离后,飞行器的姿态角的异常相较与之前明显减小 很多,滤波器变的更加稳定。
 本章小结
图 4-22 磁力计原始数据
本章小结
图 4-22 磁力计原始数据
本章首先搭建了四旋翼无人直升机飞控系统的硬件实验平台,并对所使用的传感器进行了标定,滤波处理,在硬件平台上进行了大量的实验工作,验证整体 滤波性能的好坏,给出数据对比结果,并针对飞行器在飞行过程中会有传感器数据采集异常或者有大机动的情况,运用卡方检验的方法进行检测和隔离,数据结 果显示了整个过程方法的有效性。
结 论
四旋翼直升机由于其自身灵活,机动性能好,安全性高,结构简单,易于 小型化等诸 多特点,越来越受科研工作者和航模爱好者的青睐。近年来,随着 空中机器人相关技术的提高, 以及在航空影视拍摄和农业植保领域的成功应 用,四旋翼无人机的发展将会越来越迅速 。本文在国内外前人的研究基础上 , 重点对四旋翼直升机的轨迹跟踪控制,多传感器数据融合方法和传感器数据处 理进行研究,主要包括以下几个方面的工作:
(1)依据四旋翼的动力学模型,运用卡尔曼滤波的最优估计特性,在邻 域空间估计出系统的重复性扰动和未建模误差。采用 基于时域内二次性能函数 的最优迭代学习算法,对估计出的模型误差进行扰动补偿,并用 Matlab 软件 仿真进行学习算法的评估,通过仿真给出了四旋翼无人 直升机的在各种轨迹下 的跟踪结果,证明了算法的有效性。
(2)在理论仿真完成后,本文还搭建了 四旋翼 无人直升机飞控系统的硬件实验平台,针对传感器的测量特性,对所使用的传感器进行了标定,滤波处 理,在硬件平台上进行了大量的实验工作,验证整体滤波性能的好坏,试验结 果显示所运用的 间接 卡尔曼滤波 对噪声有很好的抑制作用。最后 并针对飞行器 在飞行过程中会有传感器数据采集异常以及有大机动的情况,运用卡方检验的 方法进行 残差的 故障检测和隔离,结果证明该方法可以提高滤波器的稳定性, 系统的姿态误差在有故障时会更小。
四旋翼直升机飞控系统设计是一项长期而艰巨的任务,由于个人时间和精 力,以及实验条件的限制,本文研究还有很多扩展工作需要完善:
(1)完善飞控系统的硬件平台,采用更加精确的传感器和效果更好 的滤 波算法,同时可以 加入计算机视觉 ,为飞行器提供更加准确的 位置和姿态,让飞行器更加稳定和智能。
(2)进一步可以增加四旋翼直升机的路径规划,将迭代学习与其方法相 结合,提高系统的鲁棒性。
参考文献
[1] 党芬,王 敏芳,汪银辉. 无人机发展现状及趋势[J]. 地面防空武器,2005(3):49-54.
[2] 聂博文,马宏绪 ,王剑,等. 微小型四旋翼飞行器的研究现状与关键技术
[J]. 电光与控制,2007,14(6):113-117.
[3] 杨恩泉 , 高 金 源 . 无 人 机 机 动 轨 迹 跟 踪 系 统 设 计 [J]. 飞 行 力 学 , 2007,
25(2):30-33, 38.
[4] Bouabdallah S, Murrieri P, Siegwart R. Design and Control of an Indoor
Micro Quadrotor[C]//IEEE International Conference on Robotics and
Automation, New Orleans, USA, 2004(5):4393-4398.
[5] Altug E, Ostrowski J P, Taylor C J. Quadrotor Control Using Dual Camera
Visual Feedback[C]//IEEE International Conference on Robotics and
Automation, 2003:4294-4299.
[6] Suresh K K, Kahn A D, Yavrucuk I. GTMARS -flight Controls and Computer
Architecture[M]. Atlanta: Georgia Institute of Technology, 2000:13-21.
[7] Mellinger D, Shomin M, Kumar V. Control of Quadrotors for Robust
Perching and Landing[C]//Proceedings of the International Powered Lift
Conference, 2010:119-126.
[8] Bouabdallah S. Design and Control of Quadrotors with Application to
Autonomous Flying[D]. École Polytechnique Federale De Lausanne, 2007:
45-58.
[9] Bouabdallah S, Noth A, Siegwart R. PID vs LQ Control Techniques Applied to an Indoor Micro Quadrotor[C]//International Conference on Intelligent
Robots and Systems, 2004:2451-2456.
[10] Peng K, Cai G, Chen B M, et al. Design and Implementation of an
Autonomous Flight Control Law for a UAV Helicopter[J]. Automatica, 2009,
45(10):2333-2338.
[11] McKerrow P. Modelling the Draganflyer four -rotor helicopter[C]//IEEE International Conference on Robotics and Automation,2004:3596-3601.
[12] 刘勇,王新民 ,余翔. 基于 LQR 的直升机悬停控制律设计与仿真 [J].计算 机测量与控制,2008,16(5):670-672.
[13] Fu K. Learning Control Systems and Intelligent Control Systems: An Intersection of Artifical Intelligence And Automatic Control [J]. IEEE Transactions on Automatic Control, 1971, 16(1):70-72.
[14] Uchiyama M. Formulation of High-Speed Motion Pattern of a Mechanical
Arm by Trial[J]. Transactions on SICE (Soc. Instrum. Contr. Eng.), 1978, 14
(6):706-712.
[15] Arimoto S, Kawamura S, Miyazaki F. Bettering Operation of Robots by
Learning[J]. Journal of Robotic systems, 1984, 1(2) :123-140.
[16] Chien C J, Tayebi A. Further Results On Adaptive Iterative Learni ng Control of Robot Manipulators[J]. Automatica, 2008, 44(3):830-837.
[17] 李兵强,林辉. 抑制 PMSM 周期性转矩脉动的迭代学习方法 [J]. 电机与 控制学报, 2011, 15(9):51-55.
[18] Chen Y Q, Moore K L, Yu J, et al. Iterative Learning Control and Repetitive
Control in Hard Disk Drive Industry-A Tutorial[C]//IEEE Conference on
Decision and Control, 2006:2338-2351.
[19] Yen J Y, Yeh Y C, Peng Y H, et al. Application of the Continuous No-Reset
Switching Iterative Learning Control on a Novel Optical Scanning System [J]. Mechatronics, 2009, 19(1):65-75.
[20] Chen Y Q, Moore K L. Iterative Learning Control with Iteration-Domain
Adaptive Feed-forward Compensation[C]//The 42nd IEEE Conference on
Decision and Control, 2003:4416-4421.
[21] Lee J H, Lee K S, Kim W C. Model -based Iterative Learning Control With a
Quadratic Criterion for Time-Varying Linear Systems[J]. Automatica, 2000,
36(5):641-657.
[22] Amann N, Owens D H, Rogers E. Predictive Optimal Iterative Learning
Control[J]. International Journal of Control , 1998, 69(2):203-226.
[23] Schmidt M D. Simulation and Control of a Quadrotor U nmanned Aerial
Vehicle[D]. University of Kentucky, 2011 :15-26.
[24] Sidi M J. Spacecraft Dynamics and Control: A Practical Engineering
Approach[M]. Cambridge University Press, 1997:55-100.
[25] Leishman J G. Principles of Helicopter Aerodynamics[M] . Cambridge
University Press, 2006:55-113.
[26] Bellman R. Dynamic Programming and Lagrange Multipliers[J]. Proceedings of the National Academy of Sciences of the United States of America, 1956,
42(10): 767.
[27] Murray R, Li Z X, Sastry S S. A Mathematical Introduction to Robotic
Manipulation[M]. CRC Press, 1994:53-57.
[28] Wang B, Chen B M, Lee T H. An RPT Approach to Time-Critical Path Following of An Unmanned Helicopter[C]// IEEE Control Conference ,
2011:211-216.
[29] Madani T, Benallegue A. Control of a Quadrotor Mini-Helicopter Via Full
State Backstepping Technique[C]// The 45th IEEE Conference on Decision and Control, 2006:1515-1520.
[30] Bristow D A, Tharayil M, Alleyne A G. A Survey of Iterative Learning
Control[J]. IEEE Control Systems, 2006, 26(3):96-114.
[31] Kalman R E. A New Approach to Linear Filtering and Prediction Problems[ J].Journal of Fluids Engineering, 1960, 82(1):35-45.
[32] 蒙博宇. STM32 自学笔记[M]. 北京:北京航空航天大学出版社, 2012:298-316.
[33] Gebre-Egziabher D, Elkaim G H, David Powell J, et al. Calibration of Strapdown Magnetometers in Magnetic Field Domain [J]. Journal of Aerospace Engineering, 2006, 19(2) :87-102.
[34] Hou H. Modeling Inertial Sensors Errors Using Allan Variance[M].
University of Calgary, Department of Geomatics Engineering, 2004 :76-101. [35] El-Sheimy N, Hou H, Niu X. Analysis and Modeling of Inertial Sensors Using Allan Variance[J]. IEEE Transactions on Instrumentation and Measurement, 2008, 57(1):140-149.
[36] 熊凯,雷拥军 ,曾海波. 基于 Allan 方差法的光纤陀螺建模与仿真 [J]. 空 间控制技术与应用,2010,36(3):7-13.
[37] 赵思浩,陆明泉,冯振明. MEMS 惯性器件误差系数的 Allan 方差分析 方法[J]. 中国科学 ,2010 (5):672-675.
[38] Shynk J J. Frequency-domain and Multirate Adaptive Filtering[J]. IEEE Signal Processing Magazine,1992, 9(1):14-37.
[39] 申珊颖. 斜十字四旋翼飞行器实验建模与控制技术研究 [D]. 南京航空航 天大学,2013:15-37.
[40] Park K C, Chung D, Chung H, et al. Dead Reckoning Navigation of a Mobile Robot Using an Indirect Kalman Filter[C]// International Conference on Multisensor Fusion and Integration for Intelligent Systems , 1996:132-138. [41] 秦永元. 惯性导航[M]. 北京:科学出版社,2006:288-304.
[42] Trawny N, Roumeliotis S I. Indirect Kalman Filter for 3D Attitude
Estimation[J]. Department of Computer Science and Engineering, University of Minnesota, 2005, 26(4):8-15.
[43] 唐万生. 现代控制理论[M]. 北京: 机械工业出版社 ,1983:58-73.
[44] Brumback B, Srinath M. A Chi-Square Test for Fault-Detection in Kalman
Filters[J]. IEEE Transactions on Automatic Control, 1987, 32(6):552-554. [45] 秦永元 ,洪钺, 汪叔 华. 卡尔曼 滤波 与组 合导航 原理 [M]. 西安 :西北工业大学出版社,2012:244-252.
[46] Welch G, Bishop G. An Introduction to the Kalman Filter[J]. Proceedings of SIGGRAPH, 2001, 41(8):23175-27599.
[47] 崔乃刚,韩鹏鑫 ,穆荣军. 基于强跟踪 UKF 的导航系统故障检测方法 [J].哈尔滨工程大学学报 ,2011,32(10):1295-1299.
完整的pdf格式的设计论文51黑下载地址(完整版共53页):
 基于迭代学习的无人机的轨迹跟踪控制.pdf
(3.33 MB, 下载次数: 37)
基于迭代学习的无人机的轨迹跟踪控制.pdf
(3.33 MB, 下载次数: 37)